Giới thiệu về Mô hình toán học trong bệnh truyền nhiễm
Phùng Khánh Lâm, Ong Phúc Thịnh
Khoa YTCC - ĐHYD TPHCM, OUCRU
01/03/2023
Nội dung
Dịch tễ học bệnh truyền nhiễm
Hệ số lây nhiễm
Mô hình toán học bệnh truyền nhiễm
Dịch tễ học bệnh truyền nhiễm
Diễn tiến bệnh truyền nhiễm

Các giai đoạn của một vụ dịch
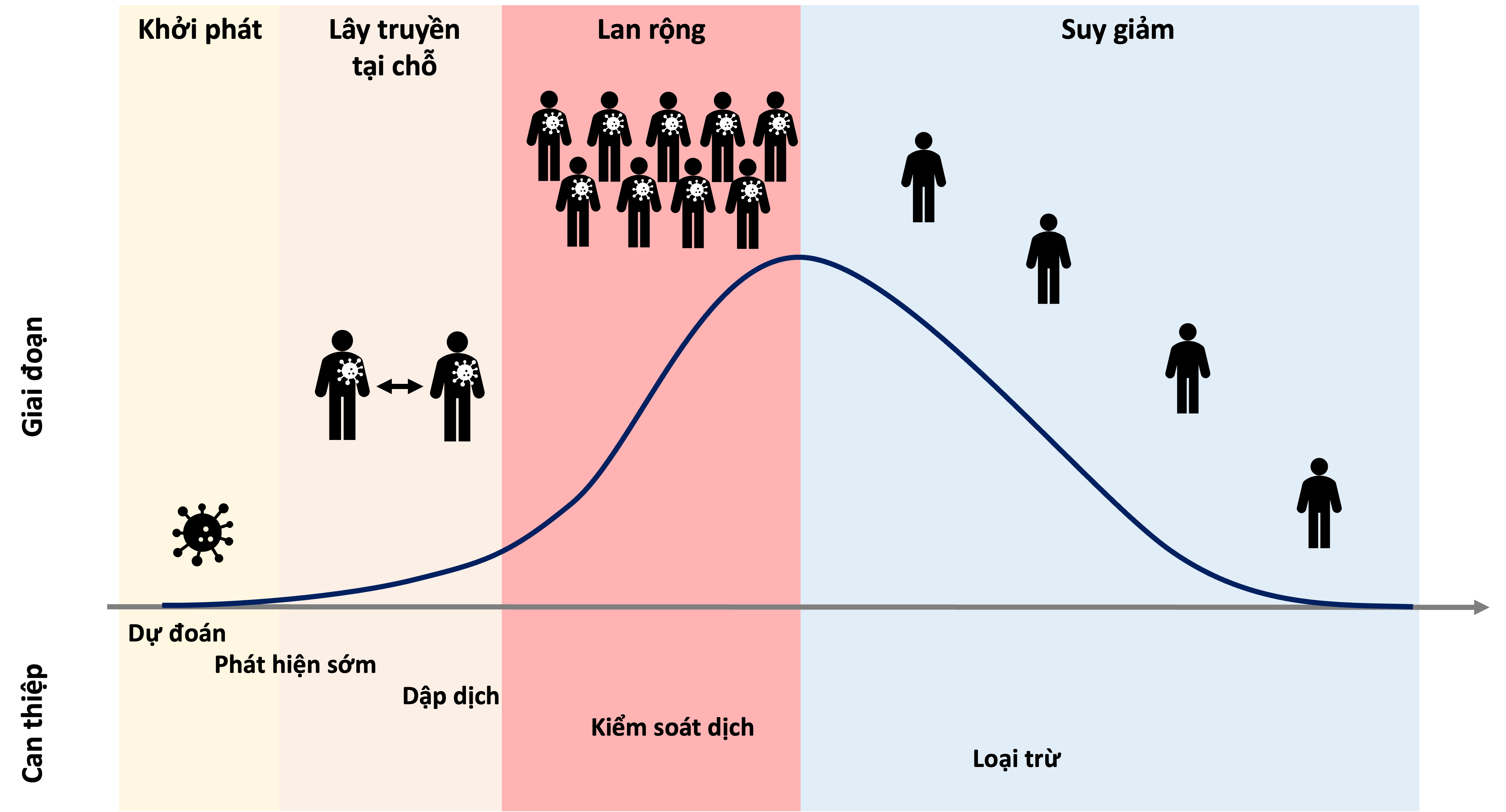
Những câu hỏi cần trả lời
Liệu vụ dịch có bùng phát hay không?
Vụ dịch sẽ có tác động như thế nào đến y tế công cộng? (mức độ nghiêm trọng của vụ dịch)
Liệu có thể kiểm soát được vụ dịch hay không?
Biện pháp nào là phù hợp để kiểm soát vụ dịch?
Liệu biện pháp can thiệp đang được sử dụng có hiệu quả không và chúng ta có thể cải thiện biện pháp này như thế nào?
Khả năng lây truyền (transmissibility) của dịch
Hệ số lây nhiễm (reproductive number, \(R\))
Tốc độ tăng trưởng của dịch (epidemic growth rate, \(r\))
Hệ số lây nhiễm \(R\)
Số ca nhiễm trung bình từ một ca nhiễm điển hình ban đầu trong suốt khoảng thời gian lây bệnh của ca nhiễm đó.
Tốc độ tăng trưởng của dịch (epidemic growth rate)
Thể hiện số ca nhiễm tăng lên trong một đơn vị thời gian.
Phụ thuộc vào hai thông số:
hệ số lây nhiễm (reproductive number)
khoảng thời gian giữa hai thế hệ lây nhiễm (generation time).
Tốc độ tăng trưởng của dịch (epidemic growth rate)
\(r\) có thể được ước tính theo công thức
\[ r = \dfrac{R-1}{Tg} \]
Với \(R\) là hệ số lây nhiễm và \(T_g\) là khoảng thời gian trung bình giữa hai thế hệ lây nhiễm.
Tốc độ tăng trưởng của dịch (epidemic growth rate)
Ở giai đoạn đầu dịch, số ca mới mắc sẽ tăng theo cấp số nhân và tỉ lệ theo:
\[exp[\frac{(R_0 - 1)}{T_g}t]\]
Với \(R_0\) là hệ số lây nhiễm cơ bản.
Thời gian thế hệ \(T_g\)
Thời gian trung bình từ lúc 1 ca bị lây nhiễm đến khi ca tiếp theo bị lây nhiễm từ ca này (khái niệm này định nghĩa theo khả năng lây nhiễm).
Thời gian thế hệ \(T_g\)

Tốc độ tăng trưởng của dịch (epidemic growth rate)
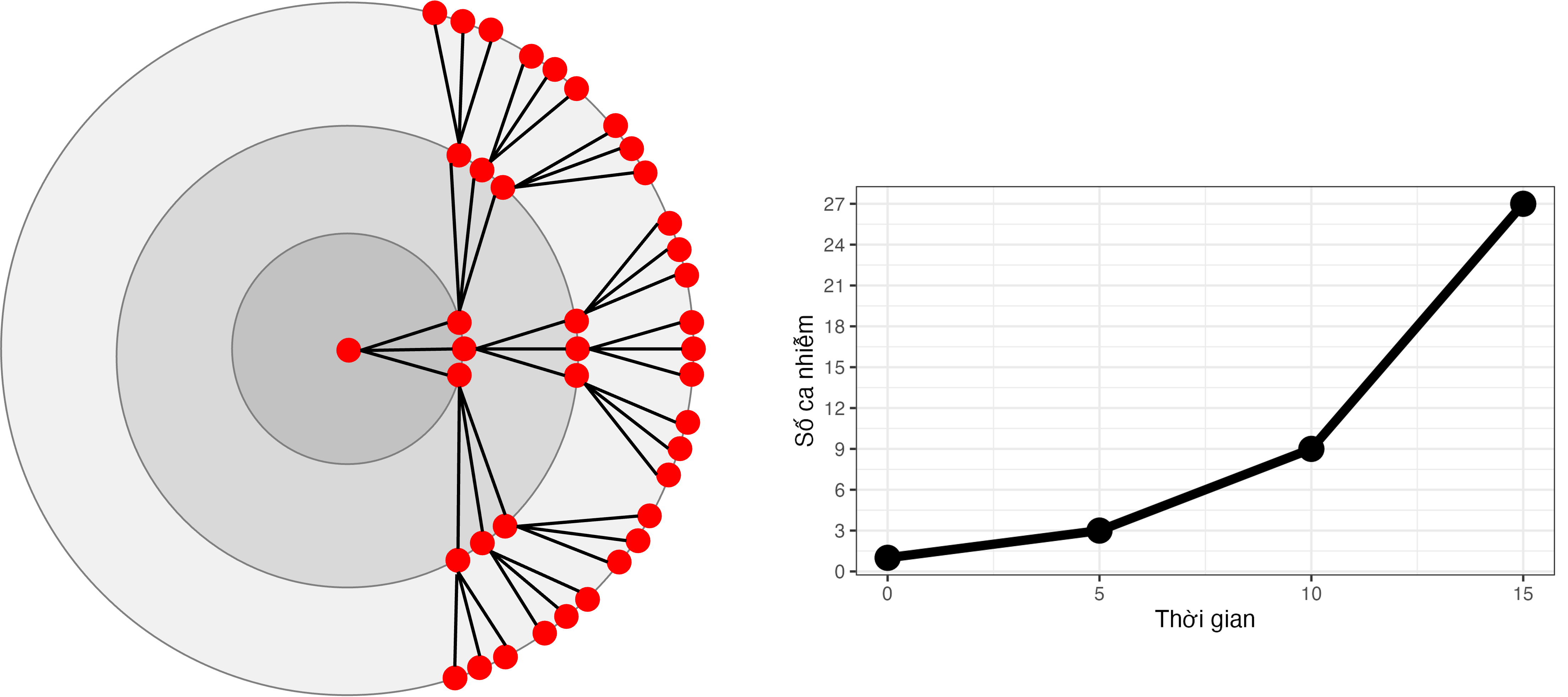
Hệ số lây nhiễm
Hệ số lây nhiễm
Số ca nhiễm trung bình từ một ca nhiễm điển hình ban đầu trong suốt khoảng thời gian lây bệnh của ca nhiễm đó.
Cần phân biệt giữa hệ số lây nhiễm cơ bản (\(R_0\)) và hệ số lây nhiễm hiệu quả (\(R_t\)).
Hệ số lây nhiễm

Hệ số lây nhiễm cơ bản (\(R_0\))
Số ca nhiễm trung bình từ một ca nhiễm điển hình ban đầu trong suốt khoảng thời gian lây bệnh của ca nhiễm đó, trong dân số hoàn toàn cảm nhiễm với bệnh (tại thời điểm dịch mới xuất hiện).
Hệ số lây nhiễm cơ bản (\(R_0\))
\(R_0\) giúp xác định khả năng lây lan của bệnh trong cộng đồng. Ví dụ về 1 bệnh nhiễm trùng không tạo miễn dịch suốt đời
Khi \(R_0\) < 1 bệnh không lây lan
Khi \(R_0\) gần bằng 1, số ca tăng dần
Khi \(R_0\) lớn, bệnh lây lan và trở thành bệnh lưu hành
Hệ số lây nhiễm cơ bản (\(R_0\))
\(R_0\) giúp xác định tốc độ lây truyền của bệnh trong cộng đồng, thông qua ước tính tốc độ tăng trưởng của dịch. \(R_0\) càng cao thì dịch có tốc độ tăng trưởng càng nhanh.
Hệ số lây nhiễm cơ bản (\(R_0\))
\(R_0\) giúp ước tính được quy mô vụ dịch khi kết thúc (\(F\))
\[ F = 1 - exp\{-R_0 \times F\} \]
\(R_0\) giúp ước tính được % số ca bệnh tại đỉnh dịch (\(H\))
\[H = 1 - \frac{1}{R_0}\]
Ngưỡng cân bằng của vụ dịch ~ mức độ can thiệp cần thiết để kiểm soát vụ dịch.
Hệ số lây nhiễm hiệu quả (\(R_t\))
Số ca nhiễm trung bình từ một ca nhiễm trong quá trình diễn tiến của vụ dịch.
Can thiệp có thể làm thay đổi \(R_t\), do đó chỉ số này được dùng để theo dõi và đánh giá hiệu quả của can thiệp.
Cách ước lượng hệ số lây nhiễm
Cần lưu ý rằng, hệ số lây nhiễm không phải là một hằng số sinh học cơ bản!
Về lý thuyết, hệ số lây nhiễm có thể được tính bằng công thức:
\[ R = D \times O \times T \times S \]
Trong đó:
\(D\) (Duration) là độ dài của thời kỳ lây nhiễm.
\(O\) (Opportunity) là cơ hội lây nhiễm, số lượng tiếp xúc trong một đơn vị thời gian.
\(T\) (Transmission probability) là xác suất lây nhiễm thành công trong một lần tiếp xúc.
\(S\) (Duration) là kích thước của dân số cảm nhiễm, % dân số có thể mắc bệnh.
Cách ước lượng hệ số lây nhiễm
Cần sử dụng nhiều loại dữ liệu khác nhau:
Dữ liệu về sự lây truyền bệnh (transmission): thường không quan sát được, thường dựa vào nghiên cứu đoàn hệ trong hộ gia đình.
Dữ liệu về kiểu tiếp xúc (contact patterns): thường khó xác định được loại hình tiếp xúc liên quan, dễ dàng nhất là đối với bệnh lây truyền qua quan hệ tình dục, thường thu thập dựa vào điều tra/dữ liệu di chuyển/dữ liệu thu thập qua app điện thoại.
Dữ liệu về lịch sử tự nhiên của bệnh.
Dữ liệu về can thiệp: từ nghiên cứu can thiệp hoặc quan sát.
Mô hình toán học bệnh truyền nhiễm
Mô hình toán học bệnh truyền nhiễm
Mô hình là sự đơn giản hoá một hệ thống phức tạp
Tất cả mọi người đều dùng mô hình 1 cách vô thức.
Mô hình toán học cho phép thực hiện được các phân tích chính xác, chặt chẽ và dự báo định lượng.
Mô hình toán học bệnh truyền nhiễm
Đối với dịch tễ học bệnh truyền nhiễm, mô hình toán học có thể dùng cho 2 nhóm mục tiêu chính:
Hiểu biết thêm về vai trò và mối quan hệ của các yếu tố khác nhau ảnh hưởng đến sự xuất hiện và diễn tiến của dịch bệnh.
Dự đoán diễn tiến của dịch bệnh.
Các bước xây dựng mô hình
Thiết kế mô hình
Ước lượng tham số
Chạy mô hình
Diễn giải kết quả
Mô hình khoang
Chia dân số thành nhiều khoang (phân nhóm)
Mỗi khoang có:
1 biến trạng thái, thể hiện số người đang ở trong khoang này, và
1 phương trình vi phân, thể hiện tần suất thay đổi của biến trạng thái
Mô hình SIR

Mô hình SIR
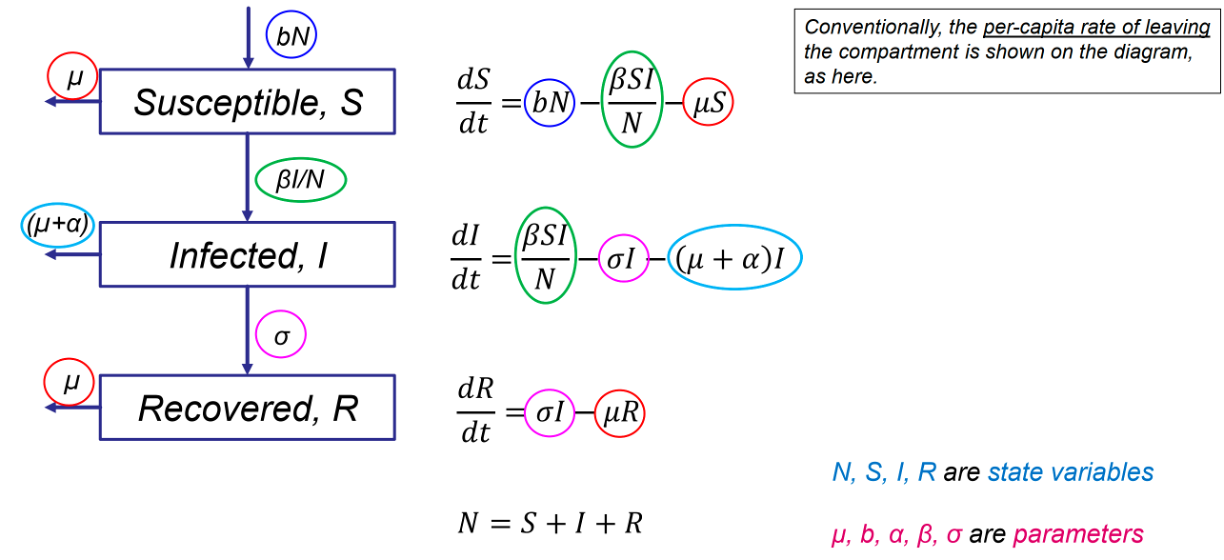
Mô hình SIR
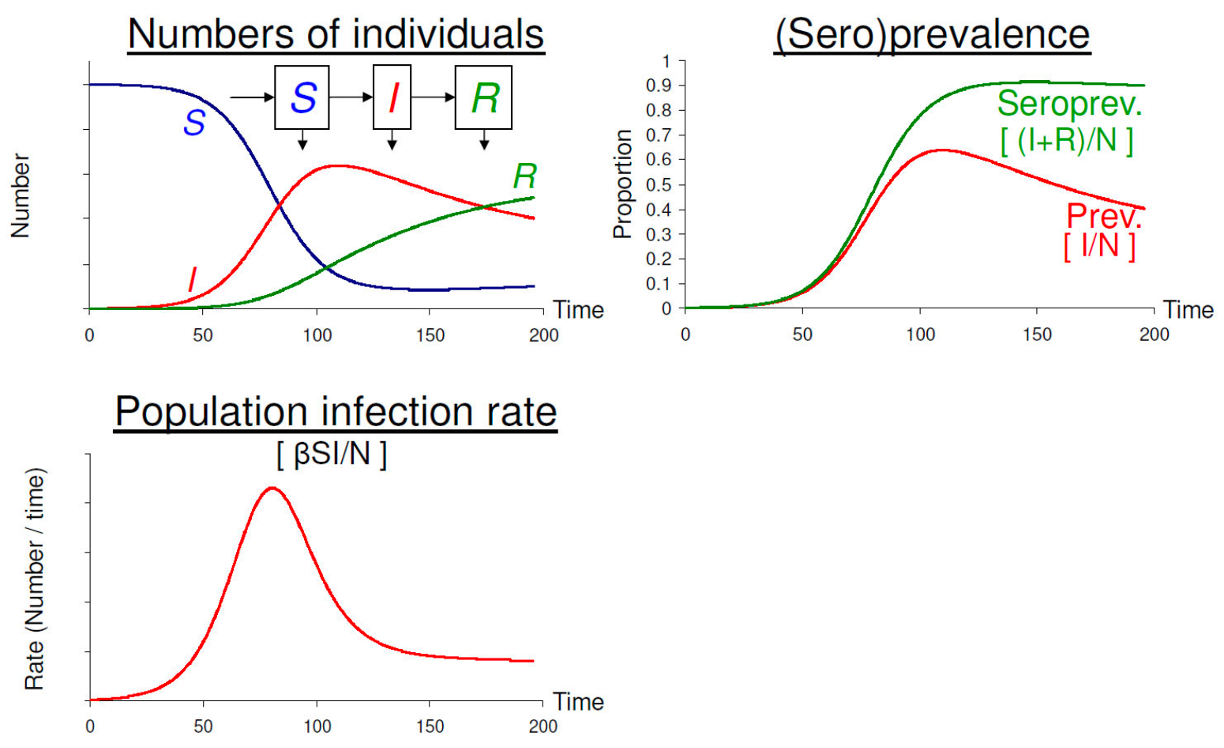
Mô hình SIR
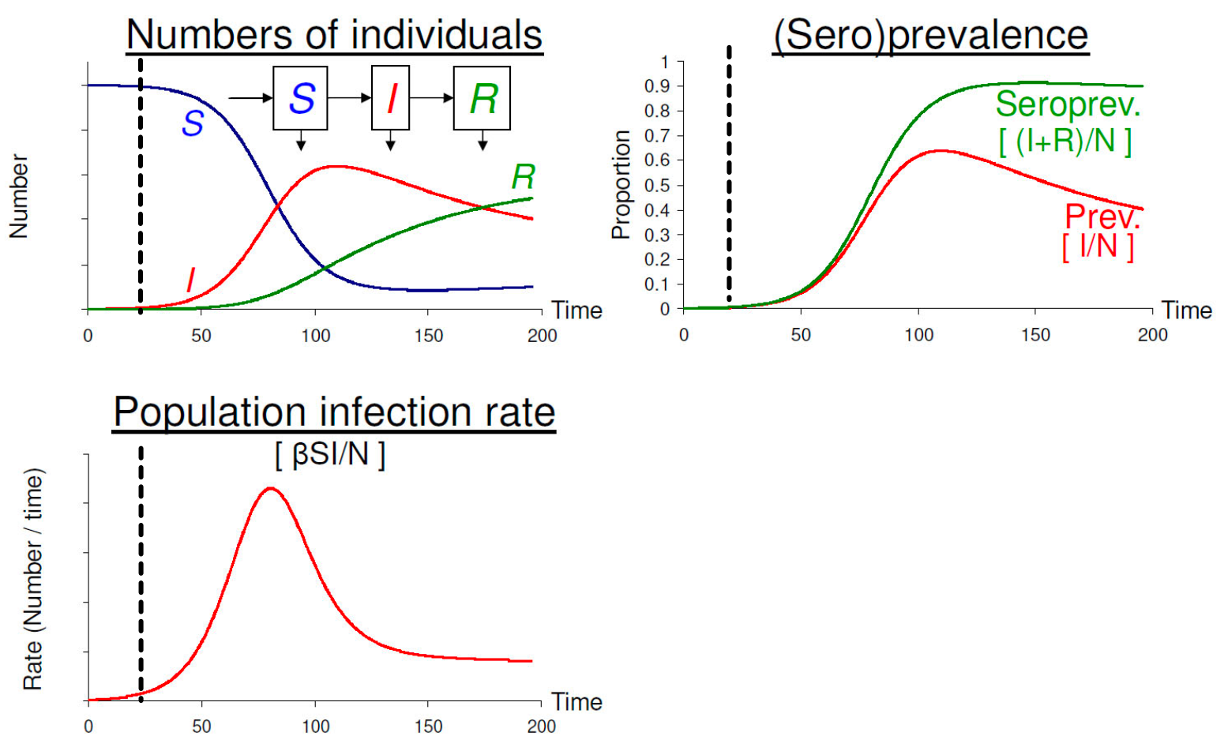
Mô hình SIR
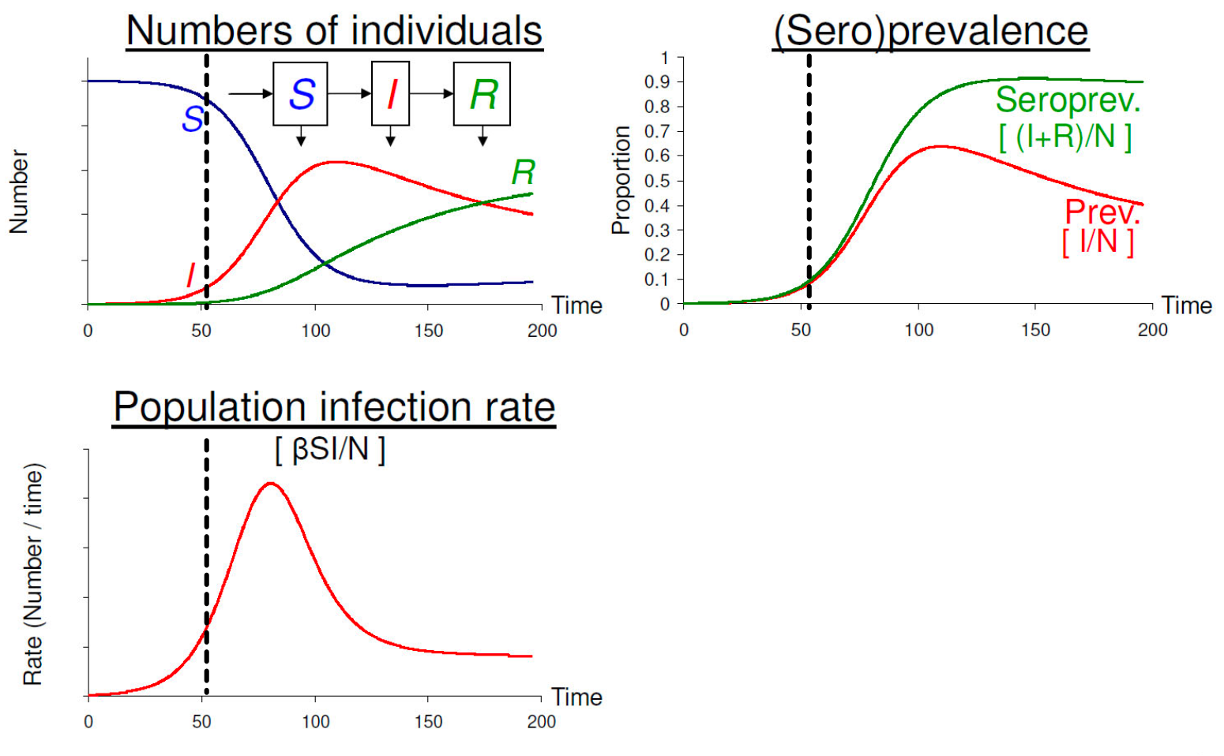
Mô hình SIR
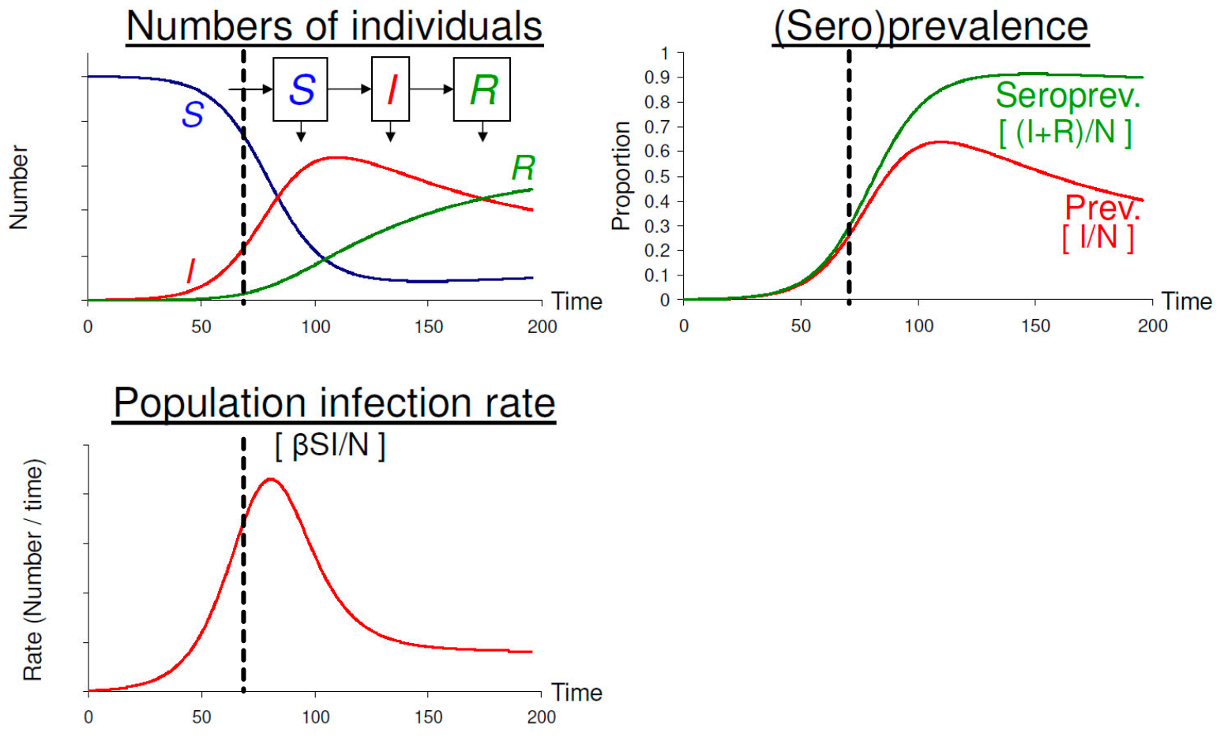
Mô hình SIR
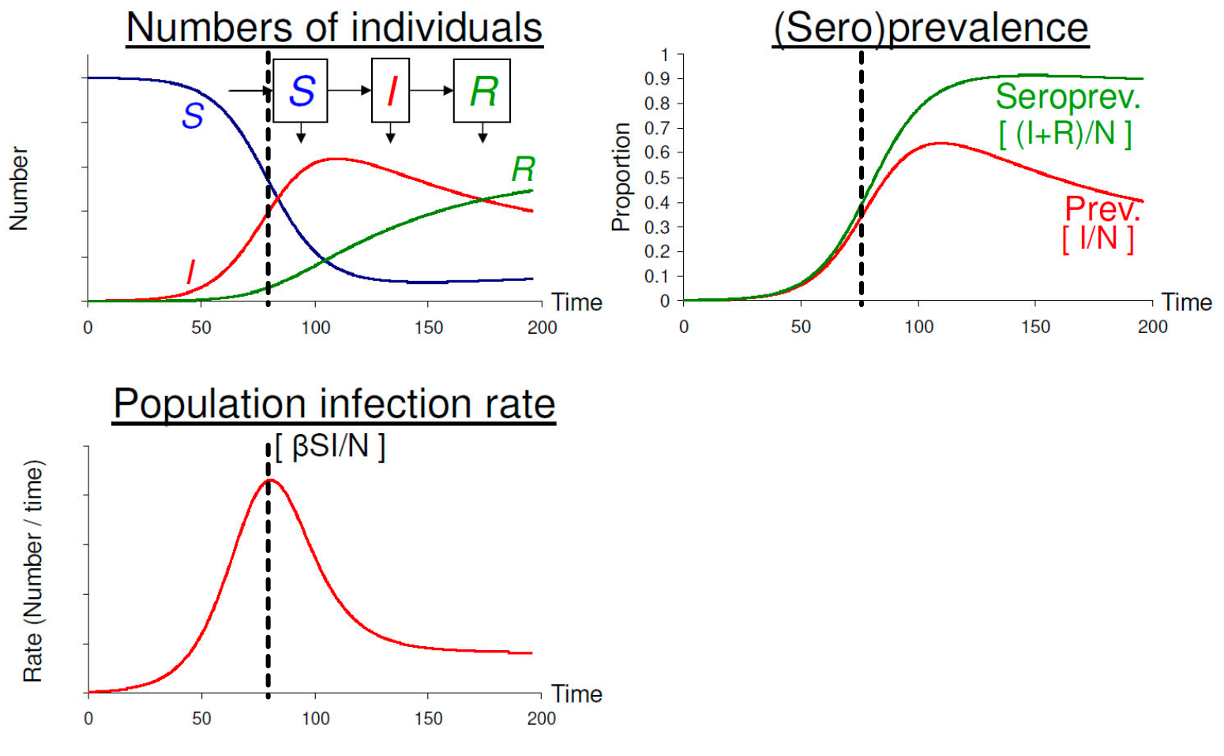
Mô hình SIR
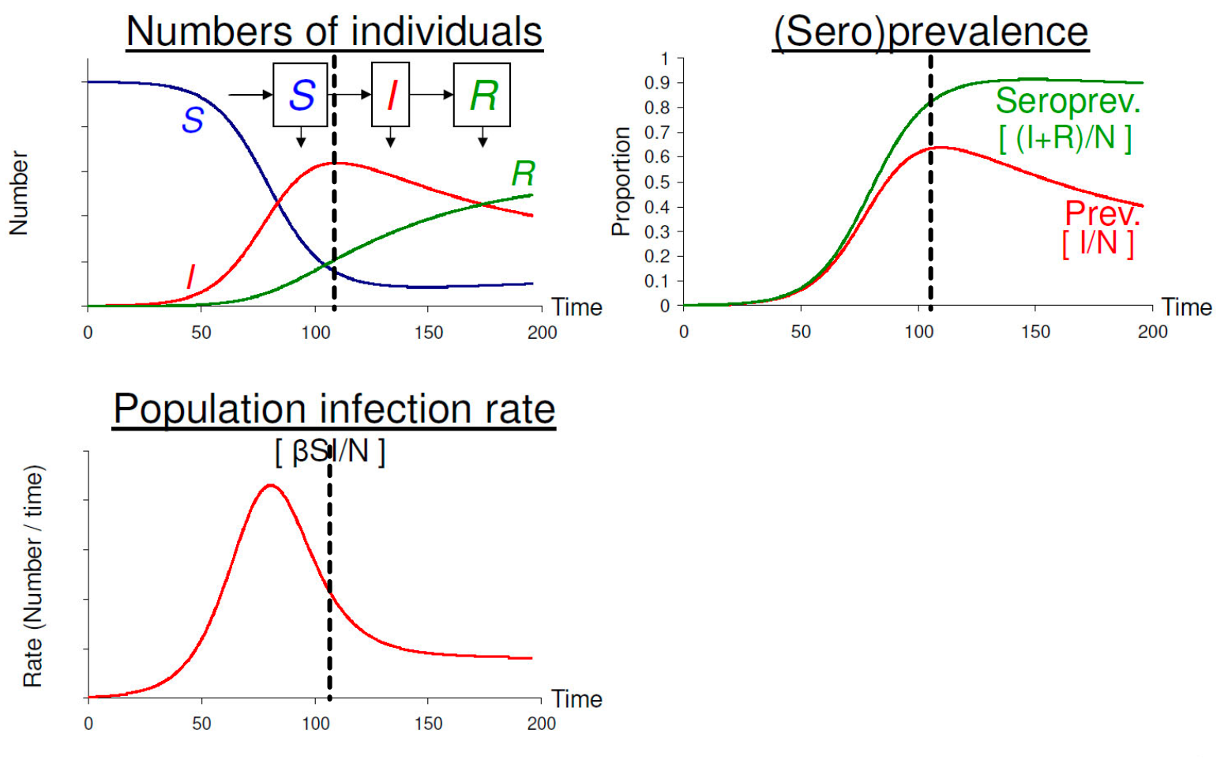
Mô hình SIR
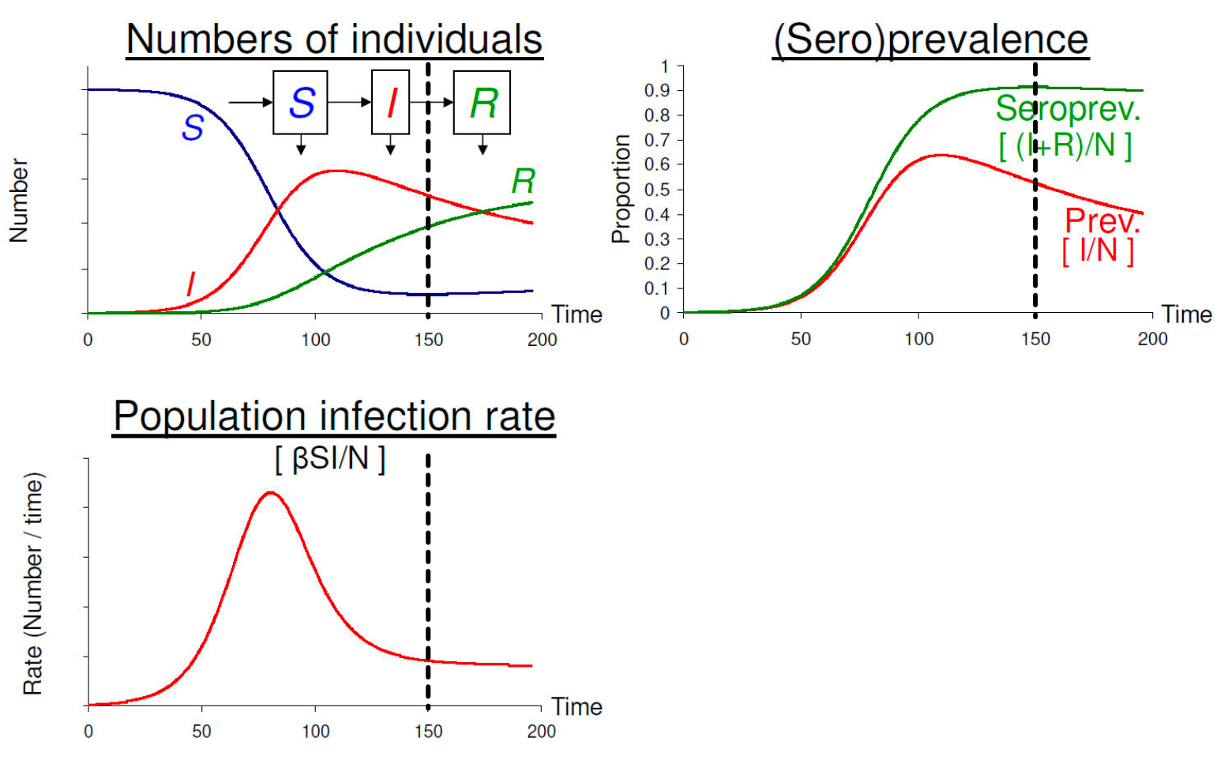
Mô hình SIR
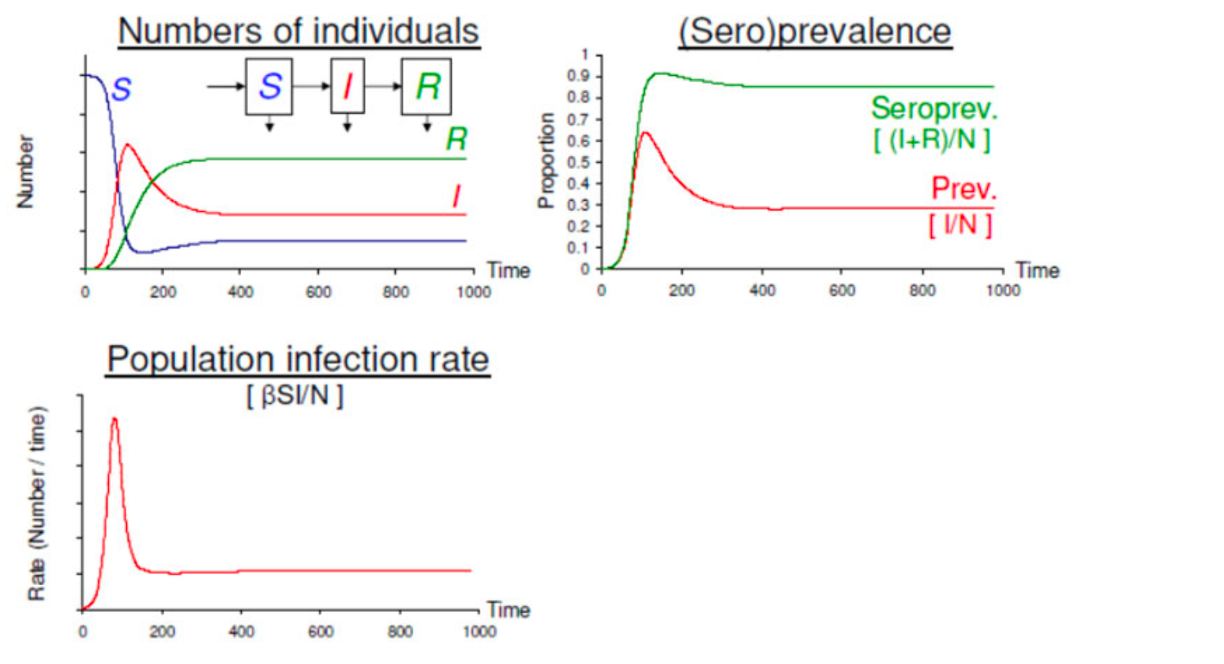
Kết luận
Kết luận
Dịch tễ học bệnh truyền nhiễm
- Khả năng lây nhiễm của bệnh
Hệ số lây nhiễm
Mô hình toán học bệnh truyền nhiễm
- Mô hình khoang
- Thiết kế, ước tính tham số (giả định)
Nội dung khoá học
https://lampk.github.io/IDMIntro